【結構ムズイ】多面体の辺や頂点の数
こんにちは(^^)/
大阪府北摂(吹田市、茨木市)の個別指導塾、優良塾宇野辺校です!
本日は正多面体の面・辺・頂点の数の求め方についてお話します。
(中学1年生の人達は予習のつもりで読んでみて下さい。3学期に習います。)
以下にまとめたのでしっかり覚えておきましょう!
| 面の数 | 辺の数 | 頂点の数 | |
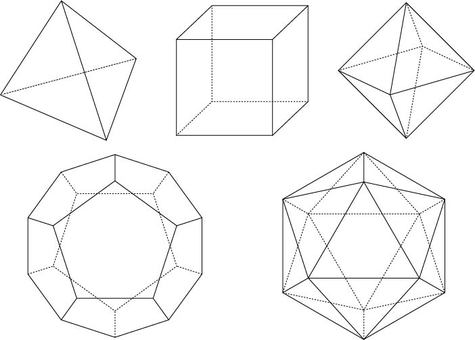
| 正四面体 | 4 | 6 | 4 |
| 正六面体 | 6 | 12 | 8 |
| 正八面体 | 8 | 12 | 6 |
| 正十二面体 | 12 | 30 | 20 |
| 正二十面体 | 20 | 30 | 12 |
…この表を見て簡単に覚えられますか?
覚えるものではありません。
本来数学とは式を使って理解するものです。
式を使って求める方法を考えてみましょう。
【面の形】
まず、正多面体の面の形はしっかりと理解しておきましょう。
正四面体 →正三角形
正六面体(=立方体) →正方形
正八面体 →正三角形
正十二面体 →正五角形
正二十面体 →正三角形
これは辺の数を考えるときにも必要になるので
図など用いながら覚えてくださいね!
【面の数】
次に面の数は大丈夫ですね?
正〇面体の数字と同じです。
これは簡単ですね!
【辺の数】
辺の数は、以下の式で求まります。
「1つの面の辺の数×面の数÷2」
これはつまり、全ての面をバラバラにしたと考えてください。
例えば正八面体は正三角形が8個集まっています。
正三角形には3本の辺があるので、バラバラ状態では合計で3×8=24本の辺があります。
これを貼り合わせると、2本の辺がそれぞれ1組になって1本になります。
よって、正八面体の辺は24÷2=12本となります。
このように辺の数を求めるには、
辺の形がわかっていないといけません。
しっかり覚えておきましょう!
覚えたら、他の正多面体の辺の数も計算してみましょう!
【頂点の数】
以下の式で求まります。
「1つの面の頂点の数×面の数÷1つの頂点に集まる面の数」
考え方は辺の数と同じで、全ての面をバラバラにしてから割るというものです。
ただし頂点の場合、複数の面の頂点が集まって立体の頂点となるので、
「÷2」ではなく「÷1つの頂点に集まる面の数」となっています。
(立体の形をイメージしてみましょう。)
…実は下に求める式も載せてますので、最後まで読んでみてね(^^)/
正四面体 →3面
正六面体(=立方体) →3面
正八面体 →4面
正十二面体 →3面
正二十面体 →5面
このことを使って、例えば正八面体の頂点の数を求めてみましょう。
正八面体は頂点に4つの面が集まるので、3×8÷4=6個です。
でも頂点に集まる面の数を考えるのはなかなか面倒ですよね…
そんなときは下に便利な公式があります
【頂点の数・別解】
もし、頂点や辺、面の数を考えるのが難しいなら、
以下の式を覚えるのも一つの手段です。
「頂点の数-辺の数+面の数=2」
これは、「オイラー式」という有名な式で、
辺の数・面の数をこの式に代入して頂点の数を求めることができます。
つまり、頂点の数が答えになるよう移項すると…
「頂点の数=辺の数-面の数+2」になります。
例えば、正八面体の頂点の数を求めてみましょう。
正八面体の辺の数は12本・面の数は8枚なので、12-8+2=6個となります。
【1つの頂点に集まる面の数】
正多角形の1つの頂点に集まる面の数について
法則性から以下の式が導けます!!!
「1つの頂点に集まる面の数=辺の数×2÷頂点の数」
例えば正八面体では…
辺の数は12、頂点の数は6なので、
12×2÷6=4 ここから頂点に集まる面の数は4つとわかります!!
他の立体も計算してみてくださいね!!
【まとめ】
如何でしたか?
正多面体の性質をイメージして理解すれば辺・頂点の個数も簡単に分かります。
図形といっても数式を使って理解を深めるのは同じです。
(立体の表面積・体積なども同じです。)
数式を使ってイメージを深め、
図形の性質をしっかりマスターしましょう!
TOPに戻る
――――――――――――――――――――――――
このブログを読んだ人にはこちらもおすすめ!
塾長はこんな人!
【生徒さん発】なんでも相談室シリーズ
塾に通ったことがない私の思う塾のメリット
超個人的!勉強おすすめ音楽!
――――――――――――――――――――――――
